[หน้าแรก] [ภาพตั้งแสดง] [ปฏิบัติการ]

             บท12 เรื่องพันธุศาสตร์ประชากร (Population Genetics)

       หัวข้อของบทเรียน
  Population
  Hardy – Weinberg Law
  การผสมพันธุ์ และ โอกาสของลูกที่เกิดแบบต่างๆ
  Codominance
  Complete dominance
  Multiple allele
 

       Population หมายถึงกลุ่มของสิ่งมีชีวิตที่ผสมพันธุ์กันได้ ตามทฤษฎีแล้วจะหมายถึงสิ่งมีชีวิตชนิด (species) เดียวกันหมด ซึ่งอาจมีการดำรงชีวิตอยู่ในสภาพภูมิศาสตร์ที่แตกต่างกันหรือห่างไกลกันแต่ก็สามารถผสมพันธุ์กันได้อย่างอิสระ  Species population ในธรรมชาติ มักจะอยู่ในสภาพภูมิศาสตร์ที่ไม่ต่อเนื่องกัน อาจมีสิ่งกีดขวางบางอย่าง ระยะห่างกัน และปัจจัยอื่น ๆ ที่ทำให้การผสมพันธุ์กันอย่างอิสระระหว่างทุก ๆ สมาชิกใน species เดียวกันไม่อาจเกิดขึ้นได้ สมาชิกมีแนวโน้มที่จะผสมกันเองในกลุ่มประชากรย่อย (subpopulation) ซึ่งเรียกว่า local populationหรือ Mendelian population ซึ่งหมายถึงกลุ่มของสิ่งมีชีวิตที่มีการผสมพันธุ์ระหว่างกัน มีส่วนร่วมในการใช้แหล่งรวมของยีน(gene pool)เดียวกัน
                                                                                                                                           [บน]

       การส่งทอดลักษณะกรรมพันธุ์แบบพันธุศาสตร์ประชากร    ตัวอย่างเช่น ประชากรแมลงหวี่ D.melanogaster ณ บริเวณใดบริเวณหนึ่งมีลักษณะกรรมพันธุ์แบบต่างๆ ที่แปรปรวนไปตาม genotypeดังนี้  ลักษณะ Dominant (homozygous) p² = 40% ลักษณะ Heterozygous  2pq = 40 % และลักษณะ Recessive q² = 20%  แมลงหวี่ในประชากรนี้จะผสมพันธุ์กันเองอย่างอิสระ(Random – mating) โอกาสที่แมลงหวี่จะผสมพันธุ์กันมีได้ 6 แบบ เช่น

             p²x p²  =  AA + AA ; p² x  2pq  = AA x Aa ; ………………..

       โอกาสแมลงหวี่จะผสมพันธุ์กัน  และมีโอกาสเกิดลูกใน generation ต่อไป เป็นตามกฎเกณฑ์ของความน่าจะเป็น (probability)

            p²     = AA        มีค่าในประชากร =          40%     (40/100)        =          0.4

            2pq  =  Aa        มีค่าในประชากร =          40%     (40/100)        =          0.4

            q²     = aa        มีค่าในประชากร  =          20%     (20/100)        =          0.2

                                                รวม          =         100%                          =          1.0

โอกาสที่เกิดการผสมพันธุ์แบบ      AA x Aa  =  0.4 x 0.4

การผสมพันธุ์แบบนี้อาจเกิดจาก    AA x Aa            หรือ      Aa x AA

การผสมพันธุ์แบบ      AA x Aa    =     2(0.4 x 0.4)

                                                  =     0.32

ลูกที่เกิดจากการผสมแบบ      AA x Aa  คือ  AA และ Aa ในอัตราส่วน ? : ?

การผสมแบบ      AA x Aa   =  0.32   ลูกที่เกิดมา เป็น AA =  0.32/2   =  0.16

                                                                                  Aa  =  0.32/2   =  0.16

       การผสมพันธุ์ในหมู่ประชากรอย่างอิสระแบบต่างๆ และโอกาสของลูกที่เกิดขึ้นจากการผสมพันธุ์เป็นดังนี้

          Gene poolหมายถึงผลรวมของ allele ทั้งหมดของยีนทุกlocusในทุกสมาชิกที่มีการผสมพันธุ์ระหว่างกันในประชากร ในช่วงเวลาใดเวลาหนึ่ง เช่น gene pool ของยีนตำแหน่งหนึ่งที่มี 3 allele คือ A₁, A₂และ A₃แต่ละสมาชิกที่เป็น diploid ก็จะมีเพียง2 allele ในแต่ละ locus สมมติให้ใน gene pool นี้มีความถี่ของยีนA₁ = 0.40, A₂ = 0.35และ A₃ = 0.25ถ้ามียีน 100 ตัว ก็จะประกอบด้วย A₁ 40 ตัว A₂ 35 ตัว และ A₃ 25 ตัว

             Hardy – Weinberg Law                                                                 [บน]

       ในปี ค.ศ. 1908 G.H. Hardy  นักคณิตศาสตร์ชาวอังกฤษ  และนักฟิสิกส์ชาวเยอรมัน ชื่อ W. Weinbergต่างศึกษาค้นคว้าปัญหาทางคณิตศาสตร์ออกมาพร้อมๆ กัน  ซึ่งมีผลต่อมารวมเรียกว่า Hardy – Weinberg Law  ซึ่งเป็นทฤษฎีที่แสดงถึงสภาพสมดุลของปริมาณของgene ในประชากรนั้น เมื่อประชากรมีขนาดใหญ่และผสมพันธุ์กันแบบอิสระ  มีเหตุผล ดังนี้

       ณ ประชากรขนาดใหญ่แห่งหนึ่ง  ที่ทำการผสมแบบอิสระและกำหนดให้ ค่าของ gene ต่างๆ ในประชากรเป็นดังนี้

p  =  ค่าของ gene A  (gene frequency of A)

q  =  ค่าของ gene a  (gene frequency of a)

และ  p  +  q   = 1

ประชากรนี้จะอยู่ในสมดุลย์ (equilibium)  เมื่อสัดส่วนของประชากรในกลุ่มนั้นเป็นดังนี้

            Homozygous Dominant         :     D    =  p²

            Heterozygous                          :      H    =  2pq

            Recessive                                :     R   =  q²

                    D  +  H  +  R                    =  p²  +  2pq  +  q²

                                    หรือ     H²    =   4DR

       เมื่อประชากรอยู่ในสมดุล  และมีการผสมพันธุ์กันต่อไปอีกกี่ชั่ว (generation) ก็ตาม  ประชากรจะอยู่ในสภาพสมดุลเสมอ

แสดงรายละเอียดของการผสมแบบสุ่มดังตารางต่อไปนี้

สรุป Genotype และ Phenotype ของลูกจากMonohybrid Cross

แบบการผสม ของ  พ่อ กับ แม่ ลูกที่เกิดจากการผสม Genotype Phenotype AA Aa Aa A-- aa AA x AA AA x Aa AA x aa      Aa x Aa Aa x aa Aa x aa 1 ? - ? - - - ? 1 2/4 ? - - - - ? ? 1 1 1 1 ? ? - - - - ? ? 1

     การผสมพันธุ์ และ โอกาสของลูกที่เกิดแบบต่างๆ                                      [บน]

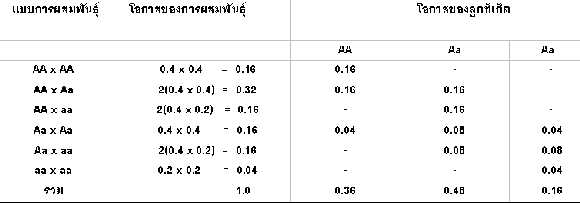     D (p² ) = 36%       H (2pq) =  48%        R (q²) =  16%

     ผลจากการผสมพันธุ์แบบอิสระได้ผล  D  =  36% ; H  =  48%  และ  R = 16% 

       เมื่อปล่อยให้ลูกที่เกิดมา  ผสมพันธุ์กันอย่างอิสระต่อไป  โอกาสของการผสมพันธุ์และโอกาสของลูกที่เกิดขึ้นเป็นดังนี้

     ผลของการผสมพันธุ์แบบอิสระได้ลูกที่เกิดมาในช่วงต่อไป เป็น  D  =  36% ;  H  =  48%  และ  R  = 16%  ซึ่งมีค่าเท่ากับช่วงที่แล้วมา ดังนั้นถ้าปล่อยให้ผสมแบบอิสระต่อไปผลของลูกที่เกิดมาในช่วงต่อไปจะคงที่เท่าเดิม  สภาพปรากฎการณ์ของลักษณะกรรมพันธุ์ต่างๆ  ที่คงที่อยู่ในช่วงต่างๆ นี้  แสดงถึงสภาพสมดุ ลของปริมาณของ gene ในประชากรนั้น

       นอกจากนั้นในประชากรที่เป็นdiploidและสืบพันธุ์แบบอาศัยเพศจะมีความถี่ของgenotypeอยู่ในสภาพสมดุล ถ้าประชากรนั้นมีการผสมพันธุ์แบบสุ่ม (random mating) มีขนาดใหญ่ ไม่มี mutation ไม่มีการอ พยพ และไม่มีการคัดเลือก เกิดเป็นกฎที่เรียกว่า Hardy-Weinberg Lawและเรียกสมดุลนี้ว่า Hardy-Weinberg equilibriumหรือ genetic equilibrium ซึ่งได้แก่

(1)  ความถี่ของ allele สมดุล

(2)  ความถี่ของ genotype สมดุล โดยความถี่ของalleleจะเป็นตัวกำหนดความถี่ของ genotypic       ถ้าสมดุลถูกรบกวนจะกลับคืนมาอีกหลังจากมีการผสมพันธุ์แบบสุ่มผ่านไป 1 ชั่วรุ่น

       ดังนั้น Hardy-Weinberg Law จึงเป็นการศึกษาพันธุกรรมของประชากรหนึ่งที่มีการผสมพันธุ์กันแบบสุ่ม(random matings) พบว่าจะมีความถี่ของยีนและยีโนไทป์อยู่ในสภาพสมดุล  เมื่อประชากรนั้นมีขนาดใ หญ่ ไม่มีการเกิดการกลายพันธุ์  ไม่มีการอพยพ และไม่มีการเกิดการคัดเลือกโดยธรรมชาติ ความถี่ของยีนหรืออัลลีลและความถีของยีโนไทป์อาจเปลี่ยนแปลงไปจากเดิม ซึ่งแต่แรกอยู่ในสภาพสมดุล จะกลับคืนมาสู่ค วามสมดุลอีกครั้งหลังจากมีการผสมพันธุ์แบบสุ่มผ่านไปหนึ่งชั่ว  (generation) ซึ่งความสมดุลของความถี่ของยีนและยีโนไทป์นี้เรียกว่าHardy-Weinberg Equilibrium

       กฎของ Hardy-Weinbergแสดงให้เห็นว่าที่สมดุลความถี่ของgenotypeจะขึ้นกับความถี่ของalleleความสัมพันธ์ระหว่างความถี่ของalleleและความถี่ของgenotypeของยีนที่ตำแหน่งใด ๆ ที่มี 2 allele แสด งไว้ในภาพที่ 2 ซึ่งแสดงให้เห็นความสัมพันธ์ ดังนี้

(1)  ความถี่สูงสุดของ heterozygoteคือ0.5 ซึ่งจะเกิดขึ้นเมื่อความถี่ของ A และ a เท่ากัน คือ เท่ากับ0.5

(2)  ถ้าความถี่ของยีนอยู่ระหว่าง 0.33 และ 0.66 heterozygoteจะมีจำนวนมากที่สุด

(3)  เมื่อความถี่ของ alleleหนึ่งมีค่าน้อย homozygote ของ allele นี้จะเป็น genotype ที่มีความถี่น้อยที่สุด

แสดงการสมดุลทางพันธุกรรมในประชากรที่มีการผสมพันธุ์แบบสุ่มหลัง

จากผ่านไป 1 ชั่วรุ่น ดังแสดงในตารางด้านล่างนี้

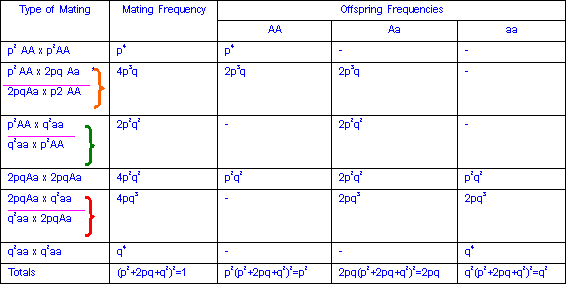
       ตัวอย่างการหาความถี่ของอัลลีลและยีโนไทป์  ซึ่งแสดงการคำนวนหาค่าความถี่ของยีนเป็นไปตามลักษณะการทำงานของยีนหลายแบบ โดยมีรายละเอียดดังต่อไปนี้

       (1) Codominance                                                                             [บน]

       เป็นลักษณะที่หาค่าความถี่ของยีนได้ง่าย เนื่องจากแต่ละ genotype จะมี phenotype ของตัวเอง เช่นลักษณะM-N blood type

ตัวอย่าง   ในการศึกษาคนอเมริกัน 6,129 คนที่อยู่ใน New York City, Boston และ Columbus, Ohio พบว่า

Phenotype Genotype Number M MN N LMLM LMLN LNLN 1,787 3,039 1,308     6,129

       สามารถหาค่าความถี่ของallele L^Mและ L^N ได้ดังนี้

ให้  p = ความถี่ของ allele L^M

       q = ความถี่ของ allele L^N

ดังนั้น    p = (2 x 1,787) + 3,039 = 0.5395
                         (2 x 6,129)

             q = (2 x 1,303) + 3,039 = 0.4605
                        (2 x 6,129)

       ความถี่ของ L^MและL^Nอาจคำนวนจากความถี่ของgenotypeก็ได้

       กฎของ Hardy-Weinbergสามารถนำมาใช้หาได้ว่าประชากรอยู่ในสมดุลหรือไม่ โดยถือว่าประชากรที่อยู่ในสมดุลจะมีความถี่ของ genotype เท่ากับ p² + 2pq + q² ในประชากรที่สามารถคำนวนหาค่าความ ถี่ของยีนด้วยวิธีดังกล่าวข้างต้น จะใช้การทดสอบ Chi-squareเพื่อตรวจสอบความสมดุลของประชากร

       (2) Complete dominance                                                                 [บน]

       เป็นลักษณะที่ heterozygote แสดงเหมือนกับ homozygous dominance ดังนั้นการหาค่าความถี่ของยีนจึงเริ่มต้นหาได้จากลักษณะ recessive ก่อน

ตัวอย่าง  ลักษณะการรู้รสของสาร PTC เกิดจากการควบคุมของยีน1 คู่  โดย taster (T) เป็น dominance ต่อ nontaster (t)จากการทดสอบนักศึกษาในมหาวิทยาลัยแห่งหนึ่งจำนวน228 คน พบว่าเป็นtaster 160 คน และ nontaster 68 คน จงหาค่าความถี่ของ allele T และ t

ให้   p = ความถี่ของ allele T

       q = ความถี่ของ allele t

Nontaster (tt) 68คน คิดเป็นความถี่        68/228 = 0.30

ดังนั้น    q² = 0.30 (ตามกฎของ Hardy-Weinberg)

             q  = ?0.30       = 0.55

             และ      p  =   1-q     = 0.45

       ความถี่ของ genotype ในประชากรนี้เมื่อมีการผสมพันธุ์แบบสุ่ม จะหาได้จาก binomial expansion p² + 2pq + q²

นั่นคือ    TT        =          p²        =          (0.45)²    =          0.20

              Tt         =          2pq      =    2(0.45)(0.55) =          0.50

              Tt         =          q²         =          (0.55)²    =          0.30

       ในกรณีนี้ไม่สามารถใช้chi-squareทดสอบว่าประชากรอยู่ในสมดุลหรือไม่ เนื่องจากการหาความถี่ของ allele ได้มาจากการถือว่าประชากรนี้อยู่ในสมดุลแล้ว จึงให้ tt =q²

       (3) Multiple allele                                                                              [บน]

       ตัวอย่างการหาความถี่ของอัลลีลและยีโนไทป์ของลักษณะหมู่เลือดABO ซึ่งมียีนที่ควบคุมเป็นแบบมัลติเพิลอัลลีล  โดยมีการถ่ายทอดพันธุกรรมของหมู่เลือดดังนี้

หมู่เลือด A      I^AI^A, I^Ai  มีการแสดงออกของgene  I^A   และ  i  เป็นแบบ  complete dominance

หมู่เลือด B      I^BI^B, I^Bi  มีการแสดงออกของgene  I^B   และ  i  เป็นแบบ  complete dominance

หมู่เลือด AB    I^AI^B            มีการแสดงออกของ gene I^A   และ  I^B  แสดงออกเท่าๆ กัน เป็นแบบ Codominance

หมู่เลือด O     i              เป็น recessive gene

       ดังนั้น ยีนที่ควบคุมหมู่เลือดมี 3 อัลลีล คือ  I^A    I^B   และ  i ในการหาความถี่ของยีน 
จึงกำหนดให้ p = ความถี่ของอัลลีล   I^A,  q =  ความถี่ของอัลลีล  I^B,  r  =  ความถี่ของอัลลีล  i

      เมื่อ   p + q + r  = 1

      ความถี่ของยีโนไทป์ในประชากรหลังจากมีการผสมพันธุ์แบบสุ่มจะเป็นดังนี้

ฟีโนไทป์ (phenotype) ยีโนไทป์ (genotype) ความถี่ยีโนไทป์ (genotypic frequency) A   IAIA IAi p2 2pr B   IBIB IBi q2 2qr O   ii r2 AB   IAIB 2pq

     วิธีการหาความถี่ของอัลลีลต่างๆ




       จากนั้นสามารถหาค่าความถี่ยีโนไทป์ (genotypic frequency) ได้
     นั่นคือ  ความถี่ยีโนไทป์ = (p + q + r)2   = p2 + q2 + 2pq + 2pr + 2qr  = 1